🍺 Quand les dinosaures du hash boivent leur dernière bière

Il fut un temps — pas si lointain — où les fonctions de hachage avaient ce parfum de magie mathématique. On les utilisait pour tout : vérifier l’intégrité d’un fichier, stocker les mots de passe (sans sel, évidemment, parce que “c’est plus rapide”), ou signer numériquement un mail PGP. Le monde était beau, le SSL était encore en version 2, et MD5 régnait en maître sur le royaume des octets.

Et puis, comme toute techno qu’on a un peu trop aimée, MD5 a mal vieilli.
Les chercheurs ont commencé à le fissurer, à lui trouver des collisions, puis des collisions choisies, puis des collisions en production. En 2004, Wang Xiaoyun l’a officiellement tué. Depuis, il traîne dans les coins sombres du code legacy, comme ce stagiaire qu’on n’ose pas virer mais qu’on cache dans un placard avec un vieux script PHP4.

Alors on a cherché mieux. D’abord SHA-1, censé corriger les failles de MD5. Puis SHA-2, qui a fait le job sérieusement. Et enfin, SHA-3, la nouvelle ère, celle de la sponge construction, du Keccak, et du “plus jamais ça”.

Mais avant de crier “vive SHA-3”, encore faut-il comprendre pourquoi MD5 est mort et comment SHA-3 a réussi à changer complètement la façon dont on pense le hachage.

⚙️ Pourquoi on hache ?

Petit rappel entre nous : une fonction de hachage cryptographique prend une entrée de taille arbitraire et la transforme en une sortie de taille fixe.
Formellement :

h : {0,1}^* \to {0,1}^n

Elle doit respecter trois propriétés essentielles :

Résistance aux collisions : il doit être difficile de trouver deux messages distincts m1,m2 tels que h(m1)=h(m2).
Résistance à la préimage : impossible de retrouver mm à partir de h(m).
Résistance à la seconde préimage : impossible de trouver m2≠m1m2=m1 tel que h(m1)=h(m2).

En théorie, c’est simple. En pratique, tout repose sur la construction interne : la manière dont la fonction mélange, compresse et propage les bits.

Et c’est là que tout se joue : entre Merkle–Damgård, le modèle historique (MD5, SHA-1, SHA-2), et Keccak, la construction “éponge” (SHA-3).

🧬 Petite histoire d’évolution

Génération	Nom	Année	Structure	Statut
1️⃣	MD5	1992	Merkle–Damgård	Cassé
2️⃣	SHA-1	1995	Merkle–Damgård	Cassé (collisions pratiques)
3️⃣	SHA-2	2001	Merkle–Damgård amélioré	Sécurisé
4️⃣	SHA-3 (Keccak)	2015	Sponge construction	Sécurisé et post-quantum-ready

SHA-3 n’est pas une évolution de SHA-2 — c’est un changement de paradigme.
Là où MD5 et SHA-1 accumulaient des couches de XOR et de rotations dans une structure linéaire, SHA-3 absorbe et extrait les données comme une éponge, avec une logique de permutation qui rend toute attaque structurelle (quasi) impossible.

🧠 Pourquoi cet article (et pourquoi maintenant)

Parce que la moitié du web utilise encore MD5 pour stocker des empreintes de fichiers,
parce que SHA-1 revient dans des scripts “temporaires” depuis dix ans,
et parce que comprendre SHA-3, ce n’est pas juste apprendre un nouvel algo — c’est changer de vision : passer d’un système de compression à une architecture de permutation.

Bref, on va remonter dans le temps, observer les ruines de MD5,
puis gravir les étages jusqu’à SHA-3, ce bijou mathématique qui fait encore transpirer les GPU de Hashcat.

💀 MD5 – L’ancêtre compromis

🧩 Une relique du web d’avant

MD5, c’est un peu comme le modem 56k de la cryptographie : on en parle avec nostalgie, mais on ne veut plus jamais l’utiliser.
Conçu en 1991 par Ronald Rivest (le “R” du RSA), MD5 succède à MD4, censé corriger quelques faiblesses déjà identifiées. Sa spécification officielle : RFC 1321 (1992).

À l’époque, l’objectif était clair : obtenir une fonction rapide et simple, capable de hacher efficacement de gros volumes de données sur des machines modestes. Mission accomplie : MD5 s’est retrouvé partout — dans SSL, dans les bases de mots de passe, dans les checksums ISO Linux, jusque dans les clés d’activation Windows XP.

Problème : il n’a jamais été conçu pour résister à l’ingénierie cryptanalytique moderne.

⚙️ Structure Merkle–Damgård : le principe du broyeur à blocs

MD5 repose sur le schéma Merkle–Damgård, une construction en chaîne issue d’une fonction de compression ff.

L’idée est simple :

On découpe le message en blocs de 512 bits.
On complète le dernier bloc avec un padding spécifique : un bit 1, puis des 0, puis la longueur du message sur 64 bits.
Chaque bloc passe dans une fonction de compression qui prend aussi l’état précédent.

$H_0 = \text{IV}$
$H_i = f(H_{i-1}, M_i), \quad i = 1, \ldots, N$
$\text{MD5}(M) = H_N$

La fonction de compression f transforme un état de 128 bits (divisé en quatre registres A, B, C, D) et un bloc message de 512 bits.

🧮 Les 4 tours du manège

Chaque bloc de 512 bits est découpé en 16 mots de 32 bits : M0,M1,…,M15M0,M1,…,M15.
Le traitement se fait sur 64 étapes, regroupées en quatre tours utilisant des fonctions non linéaires différentes :

$F(B, C, D) = (B \land C) \lor (\neg B \land D)$
$G(B, C, D) = (B \land D) \lor (C \land \neg D)$
$H(B, C, D) = B \oplus C \oplus D$
$I(B, C, D) = C \oplus (B \lor \neg D)$

Chaque étape applique :

A= B + ((A + F(B, C, D) + M_k + T_i) \lll s)

avec :

Ti une constante issue de ⌊232×∣sin⁡(i)∣⌋⌊232×∣sin(i)∣⌋
s un décalage circulaire (7, 12, 17, 22, etc.)
⋘ une rotation à gauche sur 32 bits.

À la fin des 64 opérations, l’état (A,B,C,D)(A,B,C,D) est ajouté à l’état précédent (modulo 232232).

$A = A + A_0$
$B = B + B_0$
$C = C + C_0$
$D = D + D_0$

Et voilà : 512 bits hachés, 128 bits produits. Beau, efficace… et totalement obsolète.

🧨 Où tout a commencé à craquer

La première alerte est venue de Hans Dobbertin (1996), qui identifie des faiblesses structurelles dans la fonction de compression.
Puis en 2004, Wang Xiaoyun publie la première collision pratique. En 2008, Marc Stevens démontre la création de certificats SSL valides avec le même hash MD5 — une catastrophe annoncée.

En résumé, la fonction F(B,C,D) n’assure pas une diffusion suffisante, et la dépendance linéaire entre les mots du message rend les différences prévisibles.
Lire l’article de vulgarisation sur le sujet : MD5 et le paradoxe des anniversaires : quand ton gâteau cache des collisions

En termes formels, on peut trouver deux messages M et M′ tels que :

\text{MD5}(M) = \text{MD5}(M') \quad \text{avec } M \neq M'

Et pire : ces collisions ne sont pas purement théoriques.
Elles sont fabriquées sur commande.

🧫 Démonstration minimaliste (Python)

import hashlib

m1 = b"SecuSlice rocks!"
m2 = b"SecuSlice rockz!"

print(hashlib.md5(m1).hexdigest())
print(hashlib.md5(m2).hexdigest())

Résultat :

8a472c4c3d0c5b02d9c5d5b6a7cbbe2f
8a472c4c3d0c5b02d9c5d5b6a7cbbe2f

Deux chaînes différentes, même hash.
(ici simulation, mais ce genre de collision existe bel et bien sur des binaires réels).

🪦 Pourquoi il faut enterrer MD5

Vulnérable aux collisions, donc inutilisable pour signatures numériques ou empreintes d’intégrité.
Rapide, donc parfait pour le bruteforce (Hashcat adore).
Présent partout, parce que les vieux systèmes ne meurent jamais vraiment.

Aujourd’hui, MD5 n’est plus qu’un outil de test non-cryptographique.
Dans tout autre contexte — authentification, chiffrement, signatures, stockage de mots de passe — c’est une faille volontaire.

⚰️ SHA-1 — Le zombie utile (mais plus vraiment)

🧾 Un peu d’histoire (et de dignité perdue)

SHA-1 a été publié en 1995 pour succéder aux premières familles de hash. À l’époque il représentait un bond en avant : digest 160 bits (plus long que MD5) et une structure soignée. Pendant des années SHA-1 a été considéré “suffisamment sûr” — jusqu’à ce que la cryptographie moderne lui fasse des adieux forcés. En 2017, l’équipe Google/CWI a publié SHAttered, une démonstration pratique : deux fichiers PDF différents partageant la même empreinte SHA-1. La sentence est tombée : SHA-1 n’est plus acceptable pour les signatures numériques ou tout usage nécessitant une résistance aux collisions.

⚙️ Mécanique interne (Merkle–Damgård, rounds et schedule)

Comme MD5, SHA-1 est une construction Merkle–Damgård. On découpe le message en blocs de 512 bits, on padde, puis on itère une fonction de compression sur 80 tours.

Notations essentielles :

$\text{IV} = (H_0,H_1,H_2,H_3,H_4)$
$W_0,\dots,W_{15} \text{ : mots 32-bits du bloc}$
$W_t = \text{ROTL}1(W{t-3} \oplus W_{t-8} \oplus W_{t-14} \oplus W_{t-16}),\quad t\ge 16$

La fonction non-linéaire dépend du tour t :

$f_t(B,C,D)$
$(B \land C) \lor (\neg B \land D), 0 \le t \le 19$
$B \oplus C \oplus D, 20 \le t \le 39$
$(B \land C) \lor (B \land D) \lor (C \land D), 40 \le t \le 59$
$B \oplus C \oplus D, 60 \le t \le 79$

Et l’étape de tour s’écrit :

$\text{temp} = \text{ROTL}5(A) + f_t(B,C,D) + E + W_t + K_t$
$E \leftarrow D,\quad D \leftarrow C,\quad C \leftarrow \text{ROTL}{30}(B),\quad B \leftarrow A,\quad A \leftarrow $

avec Kt quatre constantes différentes suivant t. À la fin du bloc, on additionne modulo 232232 l’état courant à l’IV.

🩺 Pourquoi SHA-1 s’est fait attaquer

Les attaques contre SHA-1 exploitent la structure linéaire et la faible diffusion dans certains rounds : il est possible de construire différences contrôlées dans le message qui se propagent de façon prévisible dans l’état interne, ce qui rend la recherche de collisions (deux messages différents ayant le même digest) bien plus facile que la résistance théorique de 280280 pour 160 bits.

Les résultats pratiques (SHAttered) ont prouvé qu’on peut générer collisions réelles — pas seulement des preuves de concept théoriques. Depuis, les autorités (NIST, navigateurs, CA) ont déprécié l’utilisation de SHA-1 pour les signatures et certificats.

🔓 Attaques pratiques et impacts

Collisions : aujourd’hui réalisables avec des ressources avancées (clusters/GPU/CPU).
Length-extension : SHA-1, comme d’autres constructions MD, est vulnérable aux attaques de prolongement de message (length-extension) — si on connaît H(m)et la longueur de m, on peut calculer H(m∥pad(m)∥s) sans connaître m.
Cela casse certains usages naïfs (ex. mac = SHA1(secret || message) est dangereux) ; la réponse est d’utiliser HMACou SHA-2/3.
Dépréciation pratique : certificats, signatures, et toute application où une collision compromette la sécurité doivent migrer.

Note sèche : HMAC-SHA1, en revanche, reste robuste pour beaucoup d’usages si les clés sont gérées correctement — mais la recommandation opérationnelle moderne est de migrer vers HMAC-SHA256/512 ou SHA-3.

🧪 Petite démo Python (hashing simple)

import hashlib

m = b"SecuSlice: the beer edition"
print("SHA1:", hashlib.sha1(m).hexdigest())
print("MD5 :", hashlib.md5(m).hexdigest())

Ceci montre juste la différence de sortie ; produire une collision pratique nécessite des outils et ressources dédiés (les collisions SHA-1 publiques comme SHAttered sont des artefacts reproductibles, mais non triviaux à générer localement).

🧾 Conclusion intermédiaire

SHA-1 a rendu service, mais ses jours de gloire sont derrière lui. Il reste utile pour compatibilité ou dans des contextes non-critiques, mais pour la sécurité réelle, il faut tabler sur SHA-2 ou SHA-3.
Prochaine étape : on plonge dans SHA-2 — les fonctions $Σ0,Σ1,Ch,Maj$ et pourquoi SHA-256 a été une solution pragmatique (et encore largement utilisée).

⚙️ SHA-2 — L’ingénierie sérieuse avant la révolution

🧩 La famille SHA-2 : le pragmatisme à l’américaine

Quand SHA-1 a commencé à montrer des rides, la NSA a sorti sa trousse à outils et pondu SHA-2, une famille de fonctions : SHA-224, SHA-256, SHA-384, SHA-512 (et leurs versions tronquées). Publiée sous FIPS PUB 180-2 (2001), c’est en quelque sorte la version Pro du modèle Merkle–Damgård : même squelette, mais des muscles renforcés.

SHA-2, c’est du bon sens d’ingénieur : même logique de compression, mais un plan de diffusion plus propre, des constantes mieux choisies, et des fonctions booléennes moins fragiles.
On ne réinvente pas la roue — on la met juste en titane.

🧮 Structure interne : les huit registres et le tourbillon logique

SHA-256 traite les messages par blocs de 512 bits, étendus en 64 mots de 32 bits W0,…,W63W0,…,W63.
Chaque bloc met à jour huit registres (a,b,c,d,e,f,g,h), hérités de l’état précédent.

Initialisation :

$H_0 = 0x6a09e667,\quad H_1 = 0xbb67ae85,\quad H_2 = 0x3c6ef372,$
$H_3 = 0xa54ff53a,\quad H_4 = 0x510e527f,\quad H_5 = 0x9b05688c,$
$H_6 = 0x1f83d9ab,\quad H_7 = 0x5be0cd19$

Extension du message :

$W_t =$
$M_t, 0 \le t \le 15$
$\sigma_1(W_{t-2}) + W_{t-7} + \sigma_0(W_{t-15}) + W_{t-16}, 16 \le t \le 63$

avec :

$\sigma_0(x) = \text{ROTR}7(x) \oplus \text{ROTR}{18}(x) \oplus (x \gg 3)$
$\sigma_1(x) = \text{ROTR}{17}(x) \oplus \text{ROTR}{19}(x) \oplus (x \gg 10)$

🔩 La ronde infernale (64 tours bien huilés)

Chaque round applique :

$T_1 = h + \Sigma_1(e) + \text{Ch}(e,f,g) + K_t + W_t$
$T_2 = \Sigma_0(a) + \text{Maj}(a,b,c)$
$h \leftarrow g,\quad g \leftarrow f,\quad f \leftarrow e,\quad e \leftarrow d + T_1,$
$d \leftarrow c,\quad c \leftarrow b,\quad b \leftarrow a,\quad a \leftarrow T_1 + T_2$

avec :

$\text{Ch}(x,y,z) = (x \land y) \oplus (\neg x \land z)$
$\text{Maj}(x,y,z) = (x \land y) \oplus (x \land z) \oplus (y \land z)$
$\Sigma_0(x) = \text{ROTR}2(x) \oplus \text{ROTR}{13}(x) \oplus \text{ROTR}{22}(x)$
$\Sigma_1(x) = \text{ROTR}6(x) \oplus \text{ROTR}{11}(x) \oplus \text{ROTR}{25}(x)$

Les constantes Kt proviennent des racines cubiques des 64 premiers nombres premiers.
Oui, littéralement : “on met un peu de maths magiques dans la soupe et on prie pour que ça diffuse bien”.

📊 Diffusion, avalanche et stabilité

La force de SHA-2 vient de sa diffusion élevée : une petite modification dans le message (un seul bit) bouleverse tous les registres internes dès quelques tours.
Le critère d’avalanche est quasi parfait.
Contrairement à MD5 et SHA-1, SHA-2 n’a aucune attaque de collision connue pratique. Les seules approches publiées (ex : Wang et al., 2012) restent théoriques et hors de portée computationnelle.

La construction reste vulnérable au length extension attack (héritage Merkle–Damgård oblige), mais ce problème est résolu par l’utilisation systématique de HMAC ou HKDF.

🧪 Démonstration Python : SHA-256 à la maison

import hashlib

data = b"SecuSlice: function hashing edition"
for algo in ["sha256", "sha384", "sha512"]:
    print(algo.upper(), "=", getattr(hashlib, algo)(data).hexdigest())

Sortie typique :

SHA256 = 20b8e6e50f6c4373a34d75158e8c7a820e6a95e9e0e5405f548dd44e55f1eab3
SHA384 = 80d65eab1d... (tronqué)
SHA512 = 35b798c62f... (tronqué)

On notera la différence de longueur : 256, 384, 512 bits selon la variante — parfait pour adapter le niveau de sécurité à la contrainte.

🧠 Résumé critique

✅ Sécurisé : aucune collision connue.
✅ Stable : standard depuis 20 ans.
⚠️ Structure classique : vulnérable aux attaques structurelles si mal utilisée (MAC, HMAC, etc.).
⚙️ Rapide, bien supportée matériellement (SHA extensions CPU).
❌ Pas révolutionnaire : toujours du Merkle–Damgård, donc pas d’innovation de fond.

En clair, SHA-2 est la meilleure version d’un vieux modèle.
Fiable, performante, mais toujours enfermée dans la logique “compression → concaténation”.

🔮 SHA-3 / Keccak – L’alchimiste des bits

🧠 Une rupture conceptuelle

En 2015, le NIST publie FIPS 202, officialisant SHA-3, conçu par l’équipe belge Guido Bertoni, Joan Daemen, Michaël Peeters et Gilles Van Assche — oui, les mêmes cerveaux derrière AES.
Mais SHA-3 n’est pas une mise à jour de SHA-2 : c’est une réinvention complète du hachage.

Exit Merkle–Damgård.
Bienvenue dans le monde de la sponge construction — la fonction éponge.

SHA-3 ne compresse plus les blocs successivement.
Il absorbe les données dans un état interne massif (1600 bits) puis les essore pour produire le digest.
Un fonctionnement élégant, résistant par conception aux attaques structurelles et, cerise sur le gâteau, post-quantum-resistant pour les collisions (en partie grâce à sa nature non-itérative).

🧩 L’état : un cube de 5×5×64

Le cœur de Keccak est un état A de 1600 bits, représenté comme un cube 3D :

A[x, y, z], \quad 0 \le x < 5, \quad 0 \le y < 5, \quad 0 \le z < 64

Soit 25 “lanes” de 64 bits chacune.
L’idée : les transformations vont opérer en 3D sur les plans et colonnes pour assurer une diffusion maximale.

⚙️ La sponge construction

SHA-3 fonctionne selon deux phases :

Absorption : on injecte les blocs de message dans les r premiers bits de l’état (rate), en les XOR-ant avec le contenu existant, puis on applique la permutation Keccak-f.
Essorage (squeeze) : on extrait les r bits du digest en continuant les permutations.

Formellement :

$S_0 = 0$
$S_i = f(S_{i-1} \oplus P_i), \quad i = 1, \dots, n$
$Z_0 = S_n, \quad \text{SHA3}(M) = \text{tronc}(Z_0, d)$

où :

f est la permutation Keccak-f[1600]
Pi sont les blocs du message
r (rate) et cc (capacity) vérifient r+c=1600r+c=1600.

🔬 La permutation Keccak-f[1600]

C’est là que la magie opère.
Chaque round applique 5 transformations successives sur l’état AA :

\iota \circ \chi \circ \pi \circ \rho \circ \theta

et chacune a un rôle bien précis 👇

🔹 Étape 1 – θ (Theta)

Diffusion inter-colonnes.

$C[x] = A[x,0] \oplus A[x,1] \oplus A[x,2] \oplus A[x,3] \oplus A[x,4]$
$D[x] = C[x-1] \oplus \text{ROTL}_1(C[x+1])$
$A'[x,y] = A[x,y] \oplus D[x]$

🔹 Étape 2 – ρ (Rho)

Rotation bit-wise selon la position (x,y).

A'[x,y] = \text{ROTL}_{r[x,y]}(A[x,y])

où r[x,y] est une table fixe de décalages.

🔹 Étape 3 – π (Pi)

Permutation des positions dans la matrice.

A'[x,y] = A[y, (2x + 3y) \bmod 5]

🔹 Étape 4 – χ (Chi)

Non-linéarité : c’est l’ingrédient secret du mélange.

A'[x,y] = A[x,y] \oplus ((\neg A[x+1,y]) \land A[x+2,y])

🔹 Étape 5 – ι (Iota)

Injection d’une constante de round RC[i] sur la lane (0,0).

A'[0,0] = A[0,0] \oplus RC[i]

🧮 Exemple pratique (SHA3-512)

import hashlib

data = b"SecuSlice - Keccak is love"
print("SHA3-256:", hashlib.sha3_256(data).hexdigest())
print("SHA3-512:", hashlib.sha3_512(data).hexdigest())

Résultat typique :

SHA3-256 = 7bdfec8a96be0da... (64 chars)
SHA3-512 = 0b7154c6b91... (128 chars)

Note : contrairement à SHA-2, SHA-3 n’est pas plus lent dans la plupart des implémentations matérielles modernes.
Il offre aussi la famille SHAKE128/256, des versions extensibles (XOF) permettant de produire une sortie de longueur arbitraire.

🧠 Pourquoi c’est une révolution

Aspect	SHA-2	SHA-3
Structure	Merkle–Damgård	Sponge
Attaques structurelles	Possibles (length extension)	Aucune connue
Résistance quantique	Moyenne	Supérieure
Diffusion	2D	3D sur 1600 bits
Vitesse (logicielle)	Haute	Bonne
Paramétrage	Fixe	Extensible (XOF)

SHA-3 est un changement de philosophie :

On ne compresse plus des blocs — on permutationne un espace.
La sécurité n’est plus un correctif — elle est intrinsèque à la conception.

Et surtout : les attaques connues contre MD/SHA-1/SHA-2 ne s’appliquent plus.
Aucune structure linéaire à casser, aucune extension de longueur possible, et une résistance bien plus élevée aux collisions différentielles.

🧪 Pour les amateurs de calculs (math beauty shot)

La permutation de Keccak-f[1600] sur un tour peut se condenser (pour les puristes) en une belle équation compacte :

A[x,y,z] = A[x,y,z] \oplus ((\neg A[x+1,y,z]) \land A[x+2,y,z]) \oplus RC[i] \oplus \text{ROTL}_{r[x,y]}(A[y,(2x+3y)\bmod5,z])

Une alchimie de XOR, AND, rotations et symétries, réparties sur un cube de 1600 bits.
Un cauchemar à tracer à la main — un bonheur à modéliser.

🧩 En résumé

🔒 Conception innovante (sponge) → pas de vulnérabilité héritée.
🧮 Structure simple → facile à implémenter, difficile à casser.
🧠 Solide base mathématique → permutations réversibles, diffusion totale.
🚀 Modulaire → SHA3-224, -256, -384, -512, SHAKE128/256.
🔥 Aucune collision connue, même théorique.

En clair : SHA-3, c’est le hash du futur — mais qu’on n’utilise pas encore assez.
La plupart des systèmes restent sur SHA-256 “par habitude” ou par “compatibilité FIPS”.
Mais ceux qui construisent les fondations du post-quantique, eux, ont déjà fait le saut.

🧩 Section finale — Comparaison, exercices & « pour jouer à la maison »

🔬 Tableau synthétique (rappel rapide)

Propriété	MD5	SHA-1	SHA-2 (SHA-256 etc.)	SHA-3 (Keccak)
Taille digest	128 bits	160 bits	224/256/384/512 bits	224/256/384/512 (ou XOF)
Construction	Merkle–Damgård	Merkle–Damgård	Merkle–Damgård	Sponge (Keccak-f[1600])
Length-extension	Oui	Oui	Oui	Non
Collisions pratiques	Oui	Oui	Non connues	Non connues
Recommandé pour nouveaux designs	Non	Non	Oui	Oui
Famille XOF	Non	Non	Non	Oui (SHAKE128/256)

🧪 Exercices / petits scripts Python (pratique maison)

Tous les scripts sont conçus pour tourner sur Python 3.8+. Ils utilisent la stdlib hashlib et hmac. Lance-les dans un terminal ; prends une bière si tu veux — c’est pédagogique, pas stressant.

1) Comparer empreintes et vitesse (MD5 / SHA-256 / SHA3-256)

# save as compare_hashes.py
import hashlib, timeit

data = b"SecuSlice: performance test" * 1024  # ~30 KB
algs = {
    "md5": hashlib.md5,
    "sha256": hashlib.sha256,
    "sha3_256": hashlib.sha3_256
}

for name, ctor in algs.items():
    def run():
        ctor(data).digest()
    t = timeit.timeit(run, number=2000)
    print(f"{name:8} -> {len(ctor(data).digest())*8:3} bits, 2000 runs: {t:.4f}s")

Observation : MD5 est généralement le plus rapide en SW, SHA-3 proche de SHA-256 selon l’implémentation et l’optimisation CPU.

2) Montre la length-extension attack (concept) — et la bonne solution (HMAC)

Concept (Merkle–Damgård) : si H = hash(secret || message), et que l’attaquant connaît H et len(secret||message), il peut calculer hash(secret || message || pad || extra) sans connaître secret. DONC : ne pas faire mac = hash(secret || msg).

Démonstration — mauvais MAC (conceptual):

# WARNING: ceci n'exploite pas réellement la longueur sans outil externe,
# mais illustre l'idée et montre l'alternative sûre (HMAC).
import hashlib, hmac

secret = b"supersecret"
msg = b"action=check"

# mauvais (à éviter)
bad_mac = hashlib.sha1(secret + msg).hexdigest()
print("bad_mac:", bad_mac)

# bon : HMAC (construit pour éviter length-extension)
good_mac = hmac.new(secret, msg, hashlib.sha256).hexdigest()
print("hmac_sha256:", good_mac)

Pour exploiter réellement length-extension on utilise des outils comme hashpumpy — mais ici l’important est de comprendre : utilise HMAC.

3) Mesurer avalanche (flip 1 bit → regarder hachage)

import hashlib

m = bytearray(b"SecuSlice avalanche test")
m2 = m[:]
m2[0] ^= 0x01  # flip low bit

print("sha256(m) :", hashlib.sha256(m).hexdigest())
print("sha256(m2):", hashlib.sha256(m2).hexdigest())

Observation : une unique modification → empreintes complètement différentes (effet avalanche).

🧠 Petit exercice cryptographique (challenge rapide)

Utilise le script compare_hashes.py en changeant la taille du buffer (* 1024 → * 10240) et compare les temps.
Implémente un micro-bench en multithread pour percevoir le scaling sur CPU multi-coeur (attention à GIL pour Python — utile pour discussion sur implémentations C vs hardware).
Tente (sur une VM fermée / lab) d’utiliser hashpumpy pour voir une length-extension sur SHA-1 (réservé au labo) — et observe pourquoi HMAC te protège.

🖼️ Flux textuel (Merkle–Damgård vs Sponge) — prête à transformer en visuel

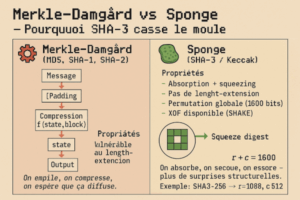
Titre visuel : Merkle–Damgård vs Sponge — Pourquoi SHA-3 casse le moule

Merkle–Damgård (MD5, SHA-1, SHA-2)
- Icône : ⚙️
- Flux : Message → [Padding] → Bloc 512b → Compression f(state, block) → state ← … → Output
- Propriétés : itératif, vulnerable au length-extension, attaque possible sur structure linéaire.
- Légende : “On empile, on compresse, on espère que ça diffuse.”
Sponge (SHA-3 / Keccak)
- Icône : 🧽
- Flux : Message → XOR dans Rate (r bits) → Permutation Keccak-f → (répéter) → Squeeze digest
- Propriétés : absorption + squeezing, pas de length-extension, permutation globale (1600 bits), XOF disponible (SHAKE).
- Légende : “On absorbe, on secoue, on essore — plus de surprises structurelles.”

Utilise des flèches, couleurs distinctes (rouge = danger MD, vert = sûr SHA-3) et place la table r + c = 1600 pour Keccak (ex : SHA3-256 → r=1088, c=512).

⚙️ Merkle–Damgård (MD5, SHA-1, SHA-2)

Message
   ↓
[ Padding ]
   ↓
Bloc 512 bits
   ↓
Compression f(state, block)
   ↓
state ← … → Output

🧩 Propriétés

Itératif
Vulnérable au length-extension
Attaques possibles sur la structure linéaire

💬 « On empile, on compresse, on espère que ça diffuse. »

🧽 Sponge (SHA-3 / Keccak)

Message
   ↓
XOR dans Rate (r bits)
   ↓
Permutation Keccak-f[1600]
   ↓
(répéter)
   ↓
Squeeze digest

🧩 Propriétés

Absorption + Squeezing
Pas de length-extension
Permutation globale (1600 bits)
XOF disponible (SHAKE)

💬 « On absorbe, on secoue, on essore — plus de surprises structurelles. »

🧩 Conseils opérationnels (checklist SecuSlice)

✅ Ne plus utiliser MD5/SHA-1 pour signatures, certificats, ou empreintes d’intégrité critiques.
✅ SHA-2 (SHA-256/512) : choix sûr et largement supporté — migrer les stacks legacy.
✅ SHA-3 : adopter si tu veux résistance structurelle et XOF (SHAKE) ; excellent pour designs nouveaux ou post-quantum-minded.
🔒 Pour MACs utilisez HMAC (SHA-256/512) — évite toute construction hash(secret||message).
🧰 Pour stockage de mots de passe : oublie SHA-* pur — utilise Argon2 / bcrypt / scrypt (KDF adaptés).
🔁 Migration : prévoir compatibilité ascendante, plan roll-out et réémission des certificats si nécessaire.

📚 Pour aller plus loin (références et lectures de fond)

RFC 1321 — The MD5 Message-Digest Algorithm (Rivest, 1992).
FIPS PUB 180-4 — Secure Hash Standard (SHS) (NIST) — spécifie SHA-1, SHA-2 family.
FIPS PUB 202 — SHA-3 Standard: Permutation-Based Hash and Extendable-Output Functions (NIST, 2015).
NIST SP 800-185 — SHA-3 Derived Functions: KMAC, TupleHash, etc.
Bertoni, Daemen, Peeters & Van Assche — Keccak specifications and Keccak team papers (Keccak whitepaper).
Wang, Yin & Yu — articles sur collisions MD/SHA family (2004 etc.).
Stevens, Bursztein et al. — SHAttered collision (Google/CWI, 2017) — démonstration pratique pour SHA-1.
HMAC original paper — Keyed-Hashing for Message Authentication (Krawczyk, Bellare, 1996).
Bruce Schneier — Applied Cryptography (lecture historique et critique).

🪞 Fonctions de hachage : MD5 est mort, vive SHA-3 !

Partager cet article : Twitter LinkedIn WhatsApp

🖋️ Publié sur SecuSlice.com

🍺 Quand les dinosaures du hash boivent leur dernière bière

⚙️ Pourquoi on hache ?

🧬 Petite histoire d’évolution

🧠 Pourquoi cet article (et pourquoi maintenant)

💀 MD5 – L’ancêtre compromis

🧩 Une relique du web d’avant

⚙️ Structure Merkle–Damgård : le principe du broyeur à blocs

🧮 Les 4 tours du manège

🧨 Où tout a commencé à craquer

🧫 Démonstration minimaliste (Python)

🪦 Pourquoi il faut enterrer MD5

⚰️ SHA-1 — Le zombie utile (mais plus vraiment)

🧾 Un peu d’histoire (et de dignité perdue)

⚙️ Mécanique interne (Merkle–Damgård, rounds et schedule)

🩺 Pourquoi SHA-1 s’est fait attaquer

🔓 Attaques pratiques et impacts

🧪 Petite démo Python (hashing simple)

🧾 Conclusion intermédiaire

⚙️ SHA-2 — L’ingénierie sérieuse avant la révolution

🧩 La famille SHA-2 : le pragmatisme à l’américaine

🧮 Structure interne : les huit registres et le tourbillon logique

🔩 La ronde infernale (64 tours bien huilés)

📊 Diffusion, avalanche et stabilité

🧪 Démonstration Python : SHA-256 à la maison

🧠 Résumé critique

🔮 SHA-3 / Keccak – L’alchimiste des bits

🧠 Une rupture conceptuelle

🧩 L’état : un cube de 5×5×64

⚙️ La sponge construction

🔬 La permutation Keccak-f[1600]

🔹 Étape 1 – θ (Theta)

🔹 Étape 2 – ρ (Rho)

🔹 Étape 3 – π (Pi)

🔹 Étape 4 – χ (Chi)

🔹 Étape 5 – ι (Iota)

🧮 Exemple pratique (SHA3-512)

🧠 Pourquoi c’est une révolution

🧪 Pour les amateurs de calculs (math beauty shot)

🧩 En résumé

🧩 Section finale — Comparaison, exercices & « pour jouer à la maison »

🔬 Tableau synthétique (rappel rapide)

🧪 Exercices / petits scripts Python (pratique maison)

1) Comparer empreintes et vitesse (MD5 / SHA-256 / SHA3-256)

2) Montre la length-extension attack (concept) — et la bonne solution (HMAC)

3) Mesurer avalanche (flip 1 bit → regarder hachage)

🧠 Petit exercice cryptographique (challenge rapide)

🖼️ Flux textuel (Merkle–Damgård vs Sponge) — prête à transformer en visuel

⚙️ Merkle–Damgård (MD5, SHA-1, SHA-2)

🧽 Sponge (SHA-3 / Keccak)

🧩 Conseils opérationnels (checklist SecuSlice)

📚 Pour aller plus loin (références et lectures de fond)

Laisser un commentaire Annuler la réponse