Le chiffrement par bloc – qu’il s’agisse de DES, AES, Blowfish, Twofish, Serpent ou Camellia – est la pierre angulaire de la cryptographie symétrique moderne et de la sécurité des données. Ces algorithmes, souvent évoqués mais rarement expliqués, transforment nos informations en blocs d’octets méconnaissables, garantissant confidentialité et intégrité dans tout ce qui touche à la cybersécurité : VPN, TLS, disques chiffrés, bases de données ou IoT.
Mais derrière les acronymes, il y a une vraie histoire d’ingénierie, de mathématiques et de guerres de standards. Entre DES, le vétéran à 56 bits, AES, l’élu du NIST, et leurs cousins oubliés, le monde du chiffrement par bloc ressemble plus à un bar de vieux hackers qu’à un cours de maths. Alors sortons les équations, les S-box, et un brin d’ironie pour revisiter les fondations de la crypto symétrique moderne — sans perdre le sens du fun.
🔲 I. DES — la vieille école
Le Data Encryption Standard (DES), c’est un peu le vinyle de la cryptographie : dépassé, mais culte.
Né dans les labos d’IBM au début des années 1970 (nom de code Lucifer, tout un programme), puis adopté par le NIST en 1977 sous la référence FIPS PUB 46, DES a régné sur les communications sécurisées pendant plus de deux décennies.
Jusqu’au jour où la puissance de calcul moderne lui a mis une claque à 56 bits près.
🧩 Notations utilisées
| Symbole | Signification |
|---|---|
| M | Message clair (plaintext) |
| C | Texte chiffré (ciphertext) |
| K | Clé secrète (56 bits utiles) |
| E_K(M) | Chiffrement du message M sous clé K |
| D_K(C) | Déchiffrement du texte C sous clé K |
| \oplus | XOR binaire |
| P(x) | Permutation |
| S_i | S-box numéro i |
| f_K(R_i) | Fonction de ronde dépendante de la clé |
🧮 Principe général
DES est un chiffrement par bloc symétrique travaillant sur 64 bits.
Chaque bloc passe par une série de transformations — permutations, substitutions, et XOR — articulées autour d’une structure de Feistel en 16 rondes.
L’idée de base :
À chaque ronde, on applique une fonction non linéaire sur la moitié droite du bloc, puis on l’additionne (XOR) à la moitié gauche.
Ensuite, on échange les deux moitiés.
Simple. Élégant. Réversible.
L’opération globale s’écrit :
(L_0, R_0) = \text{IP}(M) L_i = R_{i-1} R_i = L_{i-1} \oplus f_{K_i}(R_{i-1}) \quad \text{pour } i = 1..16 C = \text{IP}^{-1}(R_{16}, L_{16})où :
- \text{IP} est la Permutation Initiale,
- \text{IP}^{-1} est la Permutation Finale (Inverse),
- f_{K_i} applique une expansion, une substitution via 8 S-boxes, et une permutation.
🔬 Fonction de ronde f_{K_i}(R_{i-1})
C’est le cœur de DES — là où la confusion et la diffusion s’entrechoquent façon Shannon.
- Expansion :
E: R_{i-1}(32 \text{ bits}) \rightarrow 48 \text{ bits} - Mélange avec la clé de ronde :
B = E(R_{i-1}) \oplus K_i - Substitution via 8 S-boxes :
S(B) = (S_1(B_1), S_2(B_2), ..., S_8(B_8))
Chaque S_i réduit 6 bits → 4 bits. - Permutation P :
f_{K_i}(R_{i-1}) = P(S(B))
🧠 Démonstration mathématique
Le processus complet sur 16 rondes peut être représenté comme une composition de fonctions Feistel :
E_K(M) = IP^{-1} \circ F_{K_{16}} \circ F_{K_{15}} \circ ... \circ F_{K_1} \circ IP(M)avec
F_{K_i}(L, R) = (R, L \oplus f_{K_i}(R))Et la propriété magique du réseau de Feistel garantit la réversibilité :
en remplaçant K_i par K_{17-i}, on obtient directement le déchiffrement.
🧨 Limites et héritage
DES a été cassé non pas par défaut mathématique, mais par force brute :
56 bits = 2⁵⁶ ≈ 7,2×10¹⁶ clés → accessible à un cluster dès les années 1990.
C’est ce qui a motivé la création de 3DES puis d’un remplaçant plus moderne : AES.
Mais soyons honnêtes, DES a posé toutes les bases : la structure Feistel, la conception de S-boxes non linéaires, et la notion de diffusion calculée.
📚 Références documentaires
- FIPS PUB 46-3 – Data Encryption Standard (DES), NIST, 1999
- RFC 4772 – Security Implications of Using the Data Encryption Standard (DES)
- IBM Journal of Research and Development, Vol. 19, No. 5, 1975 — Lucifer Cipher Specification
- NIST Special Publication 800-67 Rev.2, 2017 – Recommendation for the Triple Data Encryption Algorithm (TDEA)
🧊 II. AES — la relève (Rijndael, le monstre élégant)
Quand DES a commencé à suer face aux clusters de brute force, le NIST a lancé un appel d’air en 1997 : il fallait un successeur.
Résultat du concours : Rijndael, développé par Vincent Rijmen et Joan Daemen (Belgique, 1998), sacré en 2001 sous le doux nom de AES – Advanced Encryption Standard (FIPS-197).
Plus moderne, plus mathématique, et surtout taillé pour le hardware comme pour le software.
🧩 Caractéristiques générales
| Élément | Valeur |
|---|---|
| Taille de bloc | 128 bits |
| Taille de clé | 128, 192 ou 256 bits |
| Structure | Substitution–Permutation (SPN) |
| Rounds | 10, 12 ou 14 selon la clé |
| Opérations | Galois Field GF(2⁸) |
| Notations | S(x) : SubBytes, P(x) : ShiftRows, M(x) : MixColumns |
AES n’est pas un Feistel. Ici, tout le bloc est transformé à chaque ronde.
La clé change, les bytes dansent, et la sécurité repose sur des mathématiques pures.
🔬 Le cœur d’AES
Chaque ronde (sauf la dernière) applique quatre opérations successives :
- SubBytes — substitution non linéaire via une S-box
- ShiftRows — décalage des lignes de l’état
- MixColumns — transformation linéaire sur chaque colonne
- AddRoundKey — XOR avec la clé de ronde
La ronde s’écrit mathématiquement ainsi :Round(State)=M(P(S(State)))⊕KiRound(State)=M(P(S(State)))⊕Ki
et la ronde finale omet la transformation MixColumns.
🧪 S-box AES complète (valeurs hexadécimales)
Elle est dérivée de l’inverse multiplicatif dans le corps de Galois GF(2⁸) combiné à une transformation affine.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 63 | 7C | 77 | 7B | F2 | 6B | 6F | C5 | 30 | 01 | 67 | 2B | FE | D7 | AB | 76 |
| 1 | CA | 82 | C9 | 7D | FA | 59 | 47 | F0 | AD | D4 | A2 | AF | 9C | A4 | 72 | C0 |
| 2 | B7 | FD | 93 | 26 | 36 | 3F | F7 | CC | 34 | A5 | E5 | F1 | 71 | D8 | 31 | 15 |
| 3 | 04 | C7 | 23 | C3 | 18 | 96 | 05 | 9A | 07 | 12 | 80 | E2 | EB | 27 | B2 | 75 |
| 4 | 09 | 83 | 2C | 1A | 1B | 6E | 5A | A0 | 52 | 3B | D6 | B3 | 29 | E3 | 2F | 84 |
| 5 | 53 | D1 | 00 | ED | 20 | FC | B1 | 5B | 6A | CB | BE | 39 | 4A | 4C | 58 | CF |
| 6 | D0 | EF | AA | FB | 43 | 4D | 33 | 85 | 45 | F9 | 02 | 7F | 50 | 3C | 9F | A8 |
| 7 | 51 | A3 | 40 | 8F | 92 | 9D | 38 | F5 | BC | B6 | DA | 21 | 10 | FF | F3 | D2 |
| 8 | CD | 0C | 13 | EC | 5F | 97 | 44 | 17 | C4 | A7 | 7E | 3D | 64 | 5D | 19 | 73 |
| 9 | 60 | 81 | 4F | DC | 22 | 2A | 90 | 88 | 46 | EE | B8 | 14 | DE | 5E | 0B | DB |
| A | E0 | 32 | 3A | 0A | 49 | 06 | 24 | 5C | C2 | D3 | AC | 62 | 91 | 95 | E4 | 79 |
| B | E7 | C8 | 37 | 6D | 8D | D5 | 4E | A9 | 6C | 56 | F4 | EA | 65 | 7A | AE | 08 |
| C | BA | 78 | 25 | 2E | 1C | A6 | B4 | C6 | E8 | DD | 74 | 1F | 4B | BD | 8B | 8A |
| D | 70 | 3E | B5 | 66 | 48 | 03 | F6 | 0E | 61 | 35 | 57 | B9 | 86 | C1 | 1D | 9E |
| E | E1 | F8 | 98 | 11 | 69 | D9 | 8E | 94 | 9B | 1E | 87 | E9 | CE | 55 | 28 | DF |
| F | 8C | A1 | 89 | 0D | BF | E6 | 42 | 68 | 41 | 99 | 2D | 0F | B0 | 54 | BB | 16 |
⚙️ Transformation MixColumns
Chaque colonne de l’état (4 octets) est considérée comme un polynôme sur GF(2⁸), multiplié par une matrice fixe :
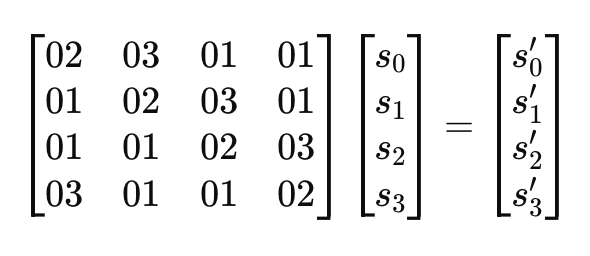
où la multiplication s’effectue dans le corps GF(2⁸) avec le polynôme irréductible x^8 + x^4 + x^3 + x + 1.
🧮 Équation générale du chiffrement AES
C=AddRoundKeyNr(SubBytes(ShiftRows(State))) après Nr rondes C=AddRoundKeyNr(SubBytes(ShiftRows(State))) après Nr rondes
avec
State = M \oplus K_0 initialement, et Nr \in {10, 12, 14}.
🧩 Exemple minimaliste (AES-128, 1ère ronde)
Si le bloc d’entrée est :
M = \text{[32 43 F6 A8 88 5A 30 8D 31 31 98 A2 E0 37 07 34]}
et la clé K_0 = \text{[2B 7E 15 16 28 AE D2 A6 AB F7 97 75 46 09 2E EA]},
alors après la première AddRoundKey :
State_1 = M \oplus K_0 = [19 A0 9A E9 3D F4 C6 F8 E3 E2 8D 48 BE 2B 2A 08]📚 Références documentaires
- FIPS PUB 197 – Advanced Encryption Standard (AES), NIST, 2001
- RFC 3602 – AES-CBC Cipher Algorithm and Block Sizes
- NIST SP 800-38A – Recommendation for Block Cipher Modes of Operation
- Daemen & Rijmen, The Design of Rijndael, Springer, 2002
🐍 III – Les cousins oubliés : Blowfish, Twofish, Serpent, Camellia
Quand AES a remporté le concours du NIST, une génération entière d’algos s’est retrouvée sur le carreau. Pourtant, ces « perdants magnifiques » ont chacun marqué l’histoire de la crypto symétrique.
🐡 Blowfish (1993, Bruce Schneier)
Le « premier couteau suisse open source » du chiffrement par bloc.
- Bloc : 64 bits
- Clé : jusqu’à 448 bits
- Structure : Feistel à 16 rondes
- S-boxes : fixées dynamiquement depuis la clé (original à l’époque)
Formule de ronde : Ri=Li−1⊕F(Ri−1,Ki),Li=Ri−1Ri=Li−1⊕F(Ri−1,Ki),Li=Ri−1
Sa fonction F est un bijou de compacité : F(x)=((S1[a]+S2[b])⊕S3[c])+S4[d]F(x)=((S1[a]+S2[b])⊕S3[c])+S4[d]
Malgré sa robustesse, son bloc trop court (64 bits) l’a rendu vulnérable au birthday bound.
Il a régné dans les années 2000 (PGP, SSH 1.3, OpenBSD) avant d’être relégué par AES et son petit frère Twofish.
Référence : Bruce Schneier – Applied Cryptography, 1996
🐠 Twofish (1998, Bruce Schneier et al.)
Finaliste du concours AES, Twofish est un Feistel hybride à 16 rondes avec blocs de 128 bits.
Il innove avec :
- des S-boxes paramétrées par la clé,
- un mélange linéaire appelé MDS matrix,
- et un pré-blanchiment/post-blanchiment du bloc.
Transformation principale : y=MDS×S(Q(x⊕Ki))y=MDS×S(Q(x⊕Ki))
Le tout sur GF(2⁸).
Il est élégant, flexible, et reste utilisé dans TrueCrypt/VeraCrypt pour ceux qui aiment chiffrer leurs disques comme en 1999.
Références : Schneier et al., « Twofish : A 128-Bit Block Cipher » (1998)
🐉 Serpent (1998, Anderson, Biham, Knudsen)
L’algorithme des puristes.
Structure SPN (Substitution-Permutation Network) de 32 rondes – paranoïa volontaire.
- Bloc : 128 bits
- Clé : jusqu’à 256 bits
- 8 S-boxes non linéaires inspirées de DES
- Chaque ronde = Substitution → Permutation → XOR avec clé
Équation : Statei+1=P(S(Statei))⊕KiStatei+1=P(S(Statei))⊕Ki
Serpent était considéré le plus conservateur du concours AES : extrêmement sûr, mais plus lent que Rijndael.
Résultat : la sécurité a perdu face à la performance.
Référence : Anderson, Biham & Knudsen, « Serpent: A New Block Cipher Proposal » (1998)
🌸 Camellia (2000, Mitsubishi & NTT, Japon)
Le plus discret mais le plus adopté en Asie.
Structure Feistel à 18 rondes, bloc 128 bits, clés 128–256 bits.
Particularités :
- opérations xor/add/sub sur GF(2⁸) et GF(2³²),
- diffusion rapide via une Matrice FL/FL⁻¹,
- performances proches d’AES,
- validé par ISO/IEC 18033-3 et RFC 3713.
Sa fonction principale : F(X,K)=P(S(X⊕K))F(X,K)=P(S(X⊕K))
Camellia est aujourd’hui intégré dans OpenSSL, GnuTLS, et le chiffrement TLS/SSH au même titre qu’AES.
⚖️ Comparatif rapide
| Algo | Bloc | Clé | Structure | Vitesse | Statut |
|---|---|---|---|---|---|
| Blowfish | 64 bits | ≤ 448 bits | Feistel | Rapide | Déprécié |
| Twofish | 128 bits | ≤ 256 bits | Feistel | Bon | Sécurisé |
| Serpent | 128 bits | ≤ 256 bits | SPN | Lent | Ultra-sûr |
| Camellia | 128 bits | ≤ 256 bits | Feistel | Excellent | ISO/NIST |
🍻 Ce qu’on en retient
Ces algos, souvent éclipsés par AES, continuent d’exister dans les stacks modernes :
- Blowfish → OpenSSH Legacy
- Twofish → VeraCrypt, GnuPG
- Serpent → VeraCrypt, OpenSSL (optionnelle)
- Camellia → TLS 1.2 / 1.3 (OpenSSL, Botan, mbedTLS)
Leur étude reste précieuse : ils incarnent les différentes philosophies de conception avant l’ère AES – le pragmatisme (Blowfish), la flexibilité (Twofish), la rigueur absolue (Serpent), et l’équilibre industriel (Camellia).
⚙️ IV – Conclusion : la vie quotidienne des blocs (OpenSSL, Botan, mbedTLS, & co)
Ce qu’il faut retenir ?
Le chiffrement par bloc n’est pas qu’un sujet de thèse : il tourne partout, tout le temps — dans ton navigateur, ton VPN, ton disque chiffré, ton smartphone et même ton badge d’accès.
Et sous le capot, ce sont les bibliothèques open source qui tiennent la baraque.
🧰 Les briques logicielles
- OpenSSL : la référence historique, implémente AES, 3DES, Camellia, Blowfish, Twofish, et même IDEA pour les nostalgiques.
Optimisé en assembleur, il exploite les instructions AES-NI des CPU modernes.
Exemple :openssl enc -aes-256-cbc -in secret.txt -out secret.enc -k mykey - mbedTLS : la version allégée pour embarqués (routeurs, IoT).
Entièrement en C, conçue pour compiler sans OS et sans malloc() :
AES, Camellia et DES restent présents, mais l’empreinte mémoire est minimale. - Botan : élégance C++ moderne, haut niveau d’abstraction, et support d’à peu près tout ce que les chercheurs ont pondu depuis 1995.
Intègre AES, Serpent, Twofish, Camellia, et même ARIA.
Parfait pour écrire des outils crypto clean et documentés. - libsodium : l’enfant rebelle de la bande — pas de AES par défaut (trop complexe à utiliser correctement), mais des primitives sûres comme XChaCha20 et Poly1305.
Le mot d’ordre : “secure by design”.
🔒 Les modes d’opération : CBC, CTR, GCM
Les bibliothèques n’implémentent pas seulement les algos bruts : elles gèrent aussi le mode d’enchaînement des blocs.
Chaque mode change profondément le comportement du chiffrement.
- CBC (Cipher Block Chaining) : classique, nécessite un IV aléatoire.
C_i = E_K(M_i \oplus C_{i-1}) - CTR (Counter Mode) : transforme un bloc en flux pseudo-aléatoire.
C_i = M_i \oplus E_K(\text{nonce} | \text{compteur}) - GCM (Galois Counter Mode) : combine CTR + authentification (MAC).
C_i = M_i \oplus E_K(\text{nonce} | i), \quad \text{Tag} = H(C, A)
Aujourd’hui, AES-GCM est devenu le standard de facto pour HTTPS, SSH et IPsec : rapide, sûr et matériellement accéléré.
🧠 Ce que la crypto moderne a retenu
- DES nous a appris la beauté du Feistel.
- AES nous a rappelé que les mathématiques finissent toujours par gagner.
- Twofish, Serpent et Camellia ont montré que la sécurité, c’est aussi une question de philosophie : performance, prudence ou élégance.
- Et les implémentations open source ont prouvé que la transparence est une forme de sécurité.
🔮 Et maintenant ?
La prochaine frontière ?
Les chiffrements post-quantiques et les modes authentifiés universels.
Mais les bonnes vieilles équations restent les mêmes :
et
M = D_K(C)… aussi intemporelles qu’une bière tiède en fin de conf crypto 🍺.
📚 Références complémentaires
- NIST FIPS-197 – Advanced Encryption Standard (AES)
- RFC 3602, RFC 5647, RFC 3713 – AES et Camellia pour TLS/SSH
- Botan Documentation officielle : https://botan.randombit.net
- mbedTLS Developer Guide : https://github.com/Mbed-TLS/mbedtls
- OpenSSL Official Docs : https://www.openssl.org/docs/
