🎬 Introduction
Cryptographie et mathématiques ou crypto et math : deux mots qui font fuir 90 % des lecteurs… sauf que derrière les équations qui piquent, il y a de la beauté, de l’élégance et parfois même un humour inattendu. Ici, pas de preuves de 30 pages ni de doctorat en théorie des nombres : juste des mini-démonstrations pour comprendre pourquoi la crypto moderne tient debout (ou s’effondre).
Et promis, vous allez voir que quelques XOR bien placés peuvent être plus fun qu’un Sudoku. On va dérouler ensemble 6 petites pépites mathématiques, qui expliquent mieux qu’un long discours pourquoi certains algorithmes tiennent encore, et pourquoi d’autres sont partis au cimetière de la sécurité.
🔀 Diffusion & confusion (merci Shannon)
Claude Shannon, le papa de la théorie de l’information, avait deux obsessions : diffusion et confusion.
👉 Traduction moderne : si ton chiffrement est prévisible, t’es foutu.
Petit exemple : prends un bloc de 4 bits 1010.
- Diffusion : on permute et mélange pour que chaque bit d’entrée affecte plein de bits de sortie.
- Confusion : on ajoute une substitution non linéaire (genre une S-box) pour casser les motifs trop réguliers.
💡 Résultat attendu : changer 1 bit en entrée doit donner une sortie totalement méconnaissable.
C’est ce principe qui est encore utilisé dans AES aujourd’hui : chaque rondelle de chiffrement mélange et brouille jusqu’à l’absurde.
🔗 🌀 Diffusion & confusion : le cocktail explosif de Shannon.
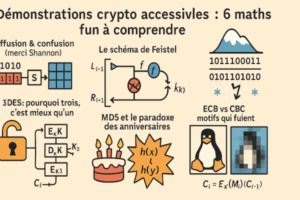
🌀 Le schéma de Feistel en poche
Le tour de magie de DES repose sur le schéma de Feistel.
Formule :
L_{i+1} = R_i
R_{i+1} = L_i \oplus f(R_i, K_i)
⚡ La beauté ? Même si la fonction f n’est pas inversible, le schéma complet l’est.
En clair : tu peux chiffrer et déchiffrer sans avoir à inverser les mathématiques de f. Ça paraît anodin, mais ça a permis de construire DES puis plein d’autres algos pratiques.
C’est comme un tour de passe-passe : on mélange, on échange, on fait une XOR party… et au final, on peut tout reconstruire. Une preuve qui tient en 3 lignes et une bière.
🔗 🪄 Le schéma de Feistel en poche — l’astuce qui rend tout réversible.
🌩️ L’effet avalanche
Imagine ton chiffrement comme une montagne de neige instable : tu changes un flocon, et tout s’écroule.
C’est l’effet avalanche. Un bon chiffrement doit rendre la sortie méconnaissable à 50 % si tu modifies un seul bit en entrée.
Exemple :
- Entrée : 10110011
- Variante : 10110001 (juste un bit changé)
- Après quelques rondes → 4 bits sur 8 ont basculé.
👉 Avalanche validée.
Sans ça, ton algorithme serait une passoire binaire : une attaque par devinette suffirait à retrouver les motifs cachés.
🔗 🌩️ L’effet avalanche — quand 1 bit fout le bordel partout.
🔐 3DES : pourquoi trois, c’est mieux qu’un
DES seul ? Game over. Sa clé de 56 bits se brute-force plus vite qu’une grille de Sudoku du dimanche.
La solution des années 90 : 3DES.
Formule magique :
C = E_{K1}(D_{K2}(E_{K1}(M)))
On appelle ça EDE (Encrypt–Decrypt–Encrypt).
⚡ Résultat : sécurité équivalente à ~112 bits. Pas parfait, mais bien plus solide.
👉 Problème : la lenteur. Et quand AES est arrivé, 3DES a pris sa retraite.
Mais sa construction reste un modèle : la preuve par composition. Même un algo bancal peut gagner en force quand on l’empile intelligemment.
🔗 🔐 3DES : pourquoi trois, c’est mieux qu’un.
🎂 MD5 et le paradoxe des anniversaires
MD5, fonction de hachage star des années 90 : 128 bits, ça paraissait incassable. Et puis… le paradoxe des anniversaires est arrivé.
👉 Dans une salle de 23 personnes, tu as 50 % de chances que deux aient le même anniversaire.
👉 Pour un hash de 128 bits, après environ 2^{64} essais, boum : collision.
Ajoute à ça des génies comme Wang Xiaoyun qui ont construit des attaques différentielles sur les rondes de MD5… et c’est fini pour lui. Aujourd’hui, l’utiliser, c’est comme signer un contrat en papier bulle.
🔗 🎂 MD5 et le paradoxe des anniversaires : quand ton gâteau cache des collisions.
📸 ECB vs CBC : motifs qui fuient
Enfin, un classique visuel : ECB contre CBC.
- ECB (Electronic Code Book) : chaque bloc est chiffré séparément. Résultat : ton image chiffrée garde les contours visibles (le fameux pingouin de la honte 🐧).
- CBC (Cipher Block Chaining) : chaque bloc dépend du précédent via un XOR → plus de motifs, le pingouin disparaît dans la neige.
⚡ Preuve par XOR :
C_i = E_K(M_i \oplus C_{i-1})
Moralité : ECB est à proscrire. À part pour les slides d’intro, ça ne sert plus à rien.
🔗 📸 ECB vs CBC : motifs qui fuient
🏁 Conclusion
Voilà un aperçu des 6 démos crypto : petites, élégantes et fun à comprendre.
- Shannon et ses obsessions : diffusion/confusion.
- Le schéma Feistel : réversible même quand f ne l’est pas.
- L’effet avalanche : un bit et tout s’effondre.
- 3DES : trois fois mieux, mais pas éternel.
- MD5 : l’exemple parfait de la chute d’un géant.
- ECB vs CBC : la preuve visuelle qui convainc même les plus sceptiques.
Ces démonstrations ne prouvent pas toute la sécurité de DES, 3DES ou MD5. Mais elles montrent la mécanique sous le capot, la logique qui rend la crypto fascinante.
👉 Pour les curieux, la suite se trouve dans les articles satellites : S-boxes, collisions construites, attaques différentielles… bref, la Saison 2 – Crypto Hardcore.
En attendant, amusez-vous avec ces mini-preuves, et souvenez-vous : la cryptographie, c’est des maths, oui. Mais c’est aussi un jeu de construction où le moindre bit peut tout faire basculer.